DAWの波形って何を表しているの？ 縦波・横波を理解しよう

― 物理の基礎から音響エンジニアの現場までをつなぐガイド ―

DAW の画面でウネウネ躍る波形、海岸で押し寄せる白波、スピーカーから内臓を揺さぶる低音――パッと見はバラバラなのに、どいつもこいつも「波」と呼ぶ。同じ言葉で括ってるけど、ホントに仲間？ …とツッコまれた瞬間、意外と説明に詰まってしまうのが人間。

高校物理を「テスト終わったら全部忘れたよ！」でスルーした人も、収録やライブを毎日回してるエンジニアも、“波って何者？” と問われると、あれ？ってなる。

そこで本ガイドは、まず 「波とは何か。」 へ原点回帰。 カギになるのは 横波・縦波・疎密波 の三兄弟。水面の波紋から、拍手が客席を走り抜ける理由、そして DAW の波形の謎まで、日常ネタでスッキリひもときます。

目指すのは 「数式アレルギーでも、読後すぐ現場でドヤれる」 記事。 さっそく 「波ってそもそも何？」 の核心へ潜っていきましょう。

波ってそもそも何？

定義： 波とは、媒質内のある点から別の点へとエネルギーを段階的に伝達する擾乱または変動のことであり、弾性的な変形や、圧力・電場または磁場の強度・電位・温度の変化などの形をとることがある。引用元：ウェブスター辞典

これだけ読んだだけだと、“波って何？”状態。そこで、実生活エピソードを元に、『あ、波ってこういうことか！』とストンと落ちる解説をお届けします。

波の性質

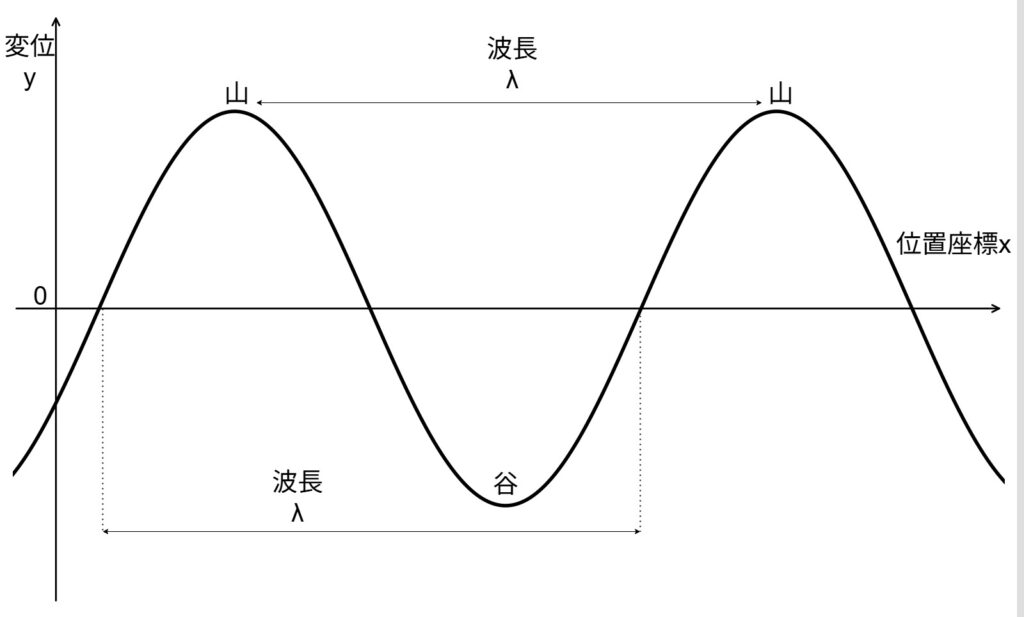
　まずはイメージから。図Aの波形は、波の山と谷が左側を開始地点として、右側に向かっていくというイメージの波形です。

この波形の横軸のどこか1点を観測すると、時間とともに「山、谷、山、谷…」とリズムを刻む様子が観測できます。

　この「山と谷の模様が次々に伝わる」現象こそが 波 。たとえば、水面に石をポチャンと放り込めば、中心から同心円状に広がる波紋が観測できます。

周囲に波を伝搬させる物質のことを “ 媒質 ” と呼び、この場合は水のことを表します。

　図Aの最大振幅*¹の点を山、最低振幅の点を谷と呼び、山と山の間隔を“ 波長 （\( \lambda \) [m])” 、山から山までの時間を“ 周期 (\(T\) [s])”、媒質が1秒間に振動する回数を“ 周波数 ”（\(f\) [Hz]） ”、波の伝わる速さを “\(V\) [m/s]” とすると、以下の関係があるといえます。

*1振幅： 物体が振動しているときの、振動の中心から最大変位までの距離。振動の幅の半分。振り幅。引用元：デジタル大辞泉

Ⅰ.周期(\(T\)[s])は周波数（\(f\) [Hz]）に反比例する

$$ T = \frac{1}{f} $$

例：50 Hz のハムノイズは \(T=1/50=0.02\) s (20 ms)。

Ⅱ.波の速さ（ \(V\)[m/s]）は、波長（\(\lambda\)[m])を周期(\(T\)[s])で割ったもの

$$ V = \frac{\lambda}{T} = \lambda f $$

つまり、波長 \( \lambda \) を周期 \( T \) で割れば進む速さV、周波数\(f\)を掛けても同じ結果が得られます。

Ⅲ.周波数から波長を逆算

$$ \lambda = \frac{v}{f} $$

例：20 kHz の高音なら \(\lambda \approx 343/20000 \approx 0.017\) m (1.7 cm)

波を構成する用語をまとめると

振幅 \(A\)	振動中心から山までの距離。単位は m（変位）や Pa（音圧）など。
波長 \(\lambda\)[m]	隣り合う山 ⇔ 山 の水平距離。単位は m。
周期 \(T\) [s]	１回の山→谷→山のサイクルに要する時間。単位は s。
周波数\(f\) [Hz]	１秒間に繰り返す山の数。単位は Hz。（\(f=1/T\)）
波の速さ\(V\)[m/s]	波が進む速さ。単位は m/s。（前述の式で求まります）

定義のおさらいと実際の現象

　ここでもう一度定義をおさらいします。

波とは、媒質内のある点から別の点へとエネルギーを段階的に伝達する擾乱または変動のことであり、弾性的な変形や、圧力・電場または磁場の強度・電位・温度の変化などの形をとることがある 。引用元：ウェブスター辞典

　 この定義の最も重要な点は、波とは「媒質中を伝わっていくゆれや変化である」ということです。波が通過する時、媒質は局所的に振動することはあっても、粒子そのものが波と一緒に移動するわけではありません。

身近な例で実感しよう

■ 水面の波紋
先ほど話した波紋について分解すると、こういった現象といえます。

1. 石がポチャンと落ちた瞬間、水面がピョコンと盛り上がり、すぐにシュルッと沈む。
2. その動きが周囲の水にも伝わり、周りの水が同じように揺れ始める。
3. こうして同心円状の波紋が広がる— 見た目は水が動いているようですが、実際には「揺れのパターン」が伝播しているだけ。

水の粒子（分子）そのものが外側へ運ばれていっているわけではありません。動いているように見えるのは「揺れの動き」であって、「水」自体ではないという点が重要です。

■ 空気中の音波

1. スピーカーから出た音が空気中を進むとき、空気分子は元の位置を中心に前後に小刻みに揺れます。
2. その揺れが次の分子に伝わり…とリレーされ、最終的に耳に到達。
3. ここでも実際に前後移動しているのは「揺れ」であって、空気がガーッと吹き飛ぶわけではありません。

※だから「音圧レベル」を測るわけで、「風速」を測ってるわけではないんです。

今説明した二つの波、実は分類が違います。

ざっくりまとめると、
水面の波紋： 横波 （Transverse wave）
空気中の音波： 縦波 （Longitudinal wave）

この２つ、媒質の「揺れる向き」が違うだけで、波の本質は同じ「揺れの伝播」です。
次はここから、縦波と横波の特徴を見ていきましょう！

横波と縦波、それぞれの特徴。

横波 (Transverse Wave)

• 媒質の振動方向と波の進行方向が垂直な波
• 媒質の各点が上下（または左右）に振動する
• 波は垂直方向の「山と谷」を次々に前方へ運ぶ
• 主な例
  • 弦の振動（ギターの弦など）
  • 水面波（プールや海のさざ波）
  • 電磁波（電波や光など、媒質を要しない横波）

縦波( Longitudinal Wave)「疎密波 Compressional / Pressure Wave」

• 媒質の振動方向と波の進行方向が平行な波
• 媒質の各点が前後に押し引きされる
• 空気の密度が濃淡になる「疎→密→疎」が連続
• 主な例
  • ばね模型
  • 空気中の音波（音源→耳）
  • 地震のP波
• 疎密波（圧力波）という呼称
  • 縦波のうち、媒質の「圧力変化」に注目して説明する場合に用いる
  • 音響工学などで一般的に用いられる。

下図は、横波と縦波（疎密波）を振動方向と進行方向の関係で比較したイメージです。

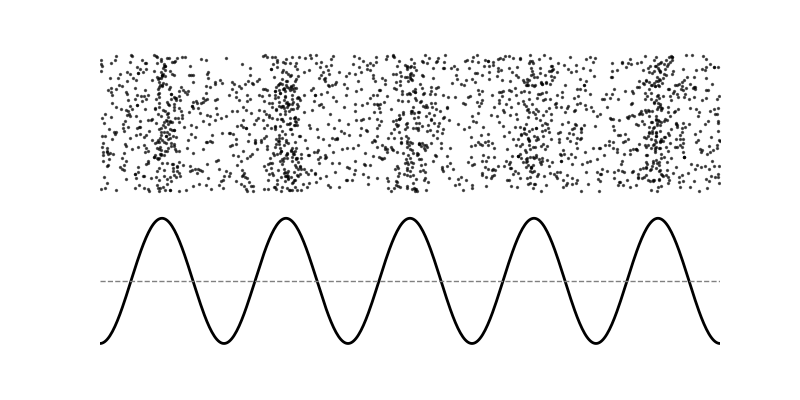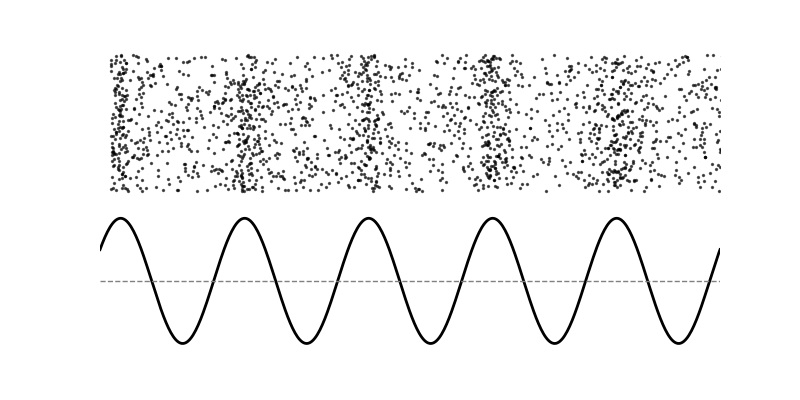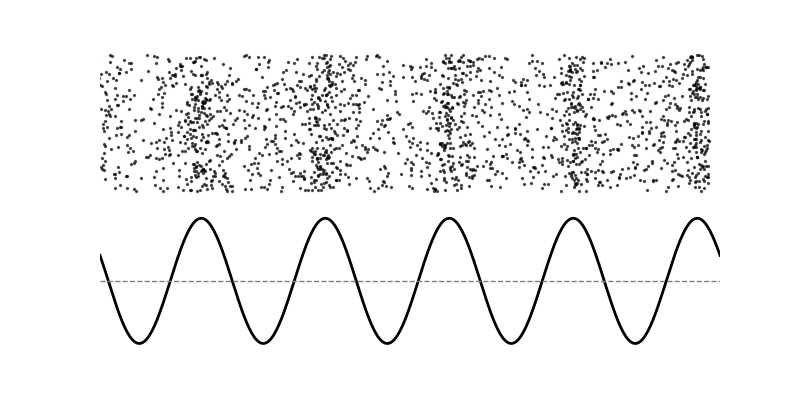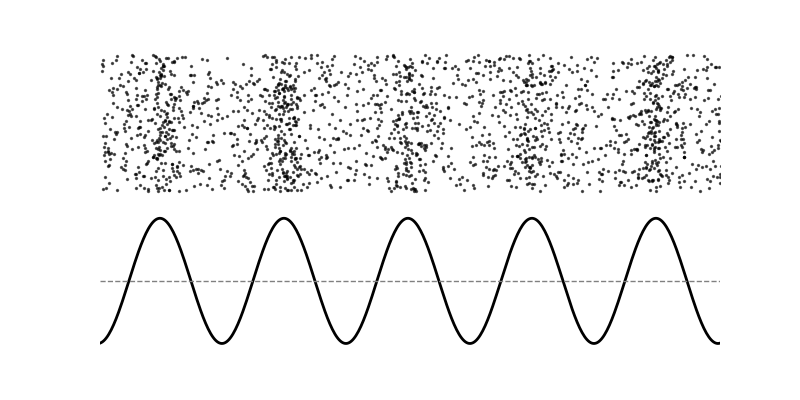
（図：横波は波の進行方向に対し媒質が上下に振動し、縦波は進行方向と同じ向きに圧縮・膨張が伝わる）

空気で「波」をイメージしてみる

キーワード	要点	身近なイメージ
媒質	波を伝える“道”となるもの――ここでは 空気分子	風船を膨らませたときの空気や場に満ちる大気
振動	分子が「ギュッ（密）⇄シュル（疎）」と前後に小刻みに揺れる。まるでドミノ倒し	スピーカーのコーンが前に押し出され、戻ってくるあのブワッとした感じ
エネルギーのリレー	揺れた分子が隣の分子にバトンタッチ…リレーのように伝播する様子が波の本体	拍手を一度叩くと、その音が遠くまで届く現象

※ 補足：実際の空気分子は通常、数十ナノメートルから数十マイクロメートル程度しか動きません。

なぜ「音波＝縦波」を“横波グラフ”で見るのか？

• 縦軸は“向き”ではなく“量”を描くキャンバス
  音波は空気の圧縮⇄膨張（前後揺れ）が起こりますが、オシロスコープやDAWでは「時間または距離に対する 圧力偏差 [Pa] 」を上下で表します。すると自然に正弦波状に見え、まるで横波のように描けちゃうんです。

まとめ ― 高校物理から現場へ一直線

1. 縦波・横波は「粒子の揺れる方向」でバッチリ区別！
   • 横波：媒質の振動方向と波の進行方向が垂直な波
   • 縦波／疎密波：媒質の振動方向と波の進行方向が平行な波
     　　　　　　：媒質が進行方向と同じ向きに圧縮⇄膨張
2. 音波は縦波だけど、DAWの波形は“圧力の山谷（上下偏差）”を横波っぽく表示しているだけ。見かけ倒しに注意！
3. 波を構成する用語[\(A\),\(\lambda\),\(T\),\(f\),V]をおさえておけば、プラグインやホワイトペーパーにしれっと記されている物理量が何を表しているのかわかります。